This is a convenient graphical representation
of the transformation equations for plane stress. Rewriting equation (A) and
(B) with all terms containing 
on one side
of the equation
equation (A) square both sides
equation (B) square both sides
This equation is of the form:
which is the equation of a circle (x2+y2
= r2) with x-axis as 
y-axis as 
,
radius as r and center of circle at (a, b).
Hence with the values of center of circle (a, b)
and radius (r) known, the plane stress equations can now be represented by the
Mohr’s circle.
Note: There are many ways to construct a circle, namely; center-radius, 3 points
on the circumference, 2 points which are diametrically opposite etc.. We shall
use the 2 points technique because it does not involve memorising of equations.
Fig. 2.8
Steps to construct a Mohr’s circle
- Locate point A.
is known and is +ve (tensile). 
is known
and is -ve, because 
the shear stress
on the surface acts is a CCW couople.
- Locate point B.
is known and is +ve (tensile). 
is known
and is +ve, because 
forms a CW couple.
- Join A and B. The line intersects the
axis at C. This is the center of the circle.
- Draw the Mohr’s circle with center at C,
using radius AC or BC.
- Note the following convention.
Normal stress: +ve (tensile); -ve (compressive)
Shear stress : 
Data obtained from a Mohr’s circle
- Principal normal stresses
and 
(equation (D)).
Since the shear stress=0 when 
and 
occurs. Therefore 
and 
must
be at the points where 
axis cuts the
Mohr's circle.
- The angle(
)
where 
and 
occurs (equation (C)).
This is half the angle measured from AC to the 
axis.
- Principal shear stress
and 
or 
(equation (F)).
- From the Mohr’s circle,
and 
are the maximum shear stress. The
corresponding occurs at point C which gives 
(equation (G)).
- The angle
,
where, 
occurs (equation (E))
This is half the angle measured from AC to the line joining 
.
Example 2
Repeat example 1 by using Mohr’s circle.
Fig. 2.9
Graphical accuracy, in general, is sufficient.
However, more accurate result, if desired, can be obtained using simple geometry
functions, with one example shown above.
Example 3
Given the state of stress shown in the Fig.2.10, locate the principal normal and
shear stress and the associated normal stress. Show the results on properly
oriented elements.
Fig. 2.10
Note that orientation of the elements can be
easily drawn by using point D which is opposite side of the 
axis of point A.
Projection of the 
, 
,
points through D would yield the surface which the respective stress acts.
Example 4
Using Mohr' s circle, transform the stresses shown in the figure into stresses
acting on the plane at an angle of 
with the
vertical axis.
Fig. 2.11
Example 5
The figure below shows a shaft and pulley system subjected to a 1kN load.
Determine the stress in Ø 25mm section.
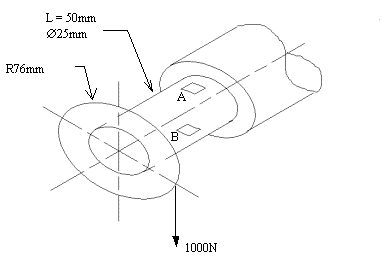
Fig. 2.12
The shaft is subjected to torsion, bending and
shear.
For Torsion
Maximum torsional stress occurs at the surface.
Using:
For Bending
Maximum BM occur at point A or B (cantilever).
MA = 1000 x 0.05
= 50 Nm
 |
 |
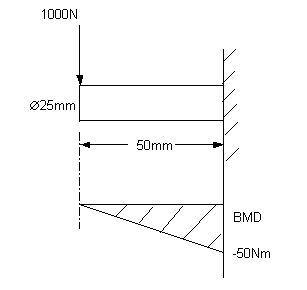The shear stresses at the surface of the shaft = 0, based on shear flow theory.
Hence the element A has the following stresses:
Construct the Mohr’s circle:
Fig. 2.13
Therefore the highest normal stress solution is
shown in Fig 2.13(i) and highest shear stress in Fig2.13(ii).
A similar solution for element B can be obtained but with the normal stress in
compressive mode.
Let us now compare the significance of using plane stress solution compared to
the conventional "one stress at a time" approach:
| |
Conventional approach |
Plane stress approach |
increase |
 |
24.77 MPa |
29.65 MPa |
19.7% |
 |
32.59 MPa |
 |
41%
 |
It is obvious that conventional approach in
combined stress analysis is clearly inadequate.The actual tensile stress
existing in element A (or on the shaft surface) has been "increase" by
41% and the shear stress by ~ 20% as compared to result obtained from
conventional calculation.
Failure of the Ø 25mm shaft will have the following characteristic:
Previous
Back
Next
