As explained earlier, there can be numerous
configurations of rosettes arrangement and each case yields different solution
of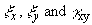 
.
Hence, it will be ideal to have a technique which can solve for the principal
strains without having to obtain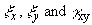 
and is applicable to a generic rosette arrangement.
This can be achieved by the technique
developed for Mohr’s circle for strain rosettes.
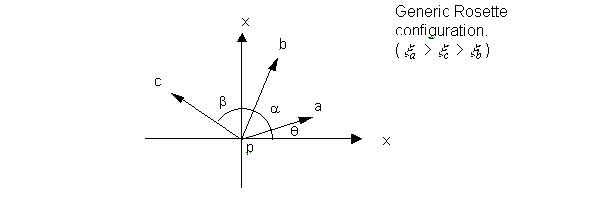
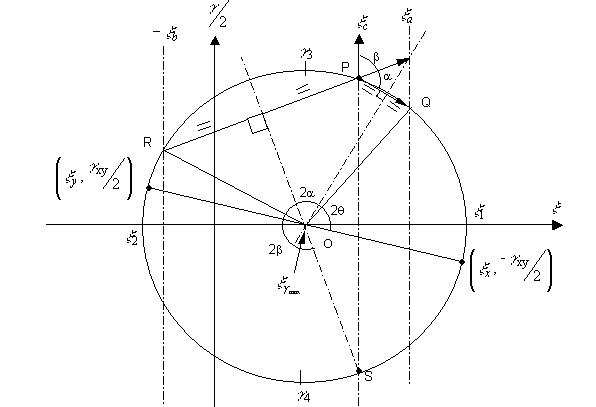
Mohr’s circle construction for strain
rosette.
Steps to construct a Mohr’s circle
for strain rosette
- Set up the vertical axis to represent
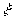= 0 which is also the 
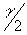axis.
- Draw 3 parallel lines to the
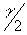axis at the appropriate distances representing the values (+ve or -ve) of 
and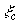 
.
- On the middle line of these three (which is
the
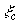line for this case), mark a point P representing the origin of the rosette.
- Draw the rosette configuration at point P
with gauge C (for this case) in line with the
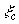line at Q and R.
- Construct perpendicular bisectors of PQ and
PR. Where these intersect is the center of the strain Mohr’s circle, O.
- Draw the circle on this center, which of
course should pass through points P, Q and R. Insert the x-axis passing
through O and this is the
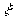axis.
- Join O to Q, R and S; where S is the
opposite point of P on the circle.
- Lines OQ, OR and OS represents the 3 gauges
on the circle where 2
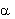and 2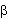
are the angles between the gauges.
- From the circle, read off the required
strain values e.g.
.
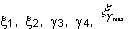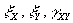can also be found by considering the appropriate angle
(
)
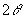from gauge a.
Example 8
Using Example 7, solve using Mohr's circle for strain rosette
Solution:
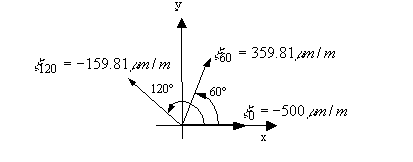
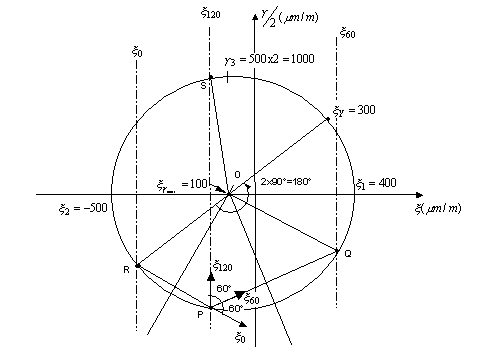
Notice that:
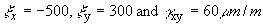which is the same as that obtained using equations in example 7.
- Principal strain solution are the same as
Mohr’s circle solution using
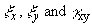values as shown in Example 6.
Hence, this construction technique of
Mohr’s circle for strain rosettes is a very powerful technique in obtaining
principal strains without the constraint of using equations for each case of
rosettes configuration.
Previous
Back